LV.NOL.2013.8.4
Kvadrātā \(3 \times 3\) rūtiņas ieraksti deviņus dažādus naturālus skaitļus tā, lai katrā rindiņā ierakstīto skaitļu reizinājums un katrā kolonnā ierakstīto skaitļu reizinājums būtu viens un tas pats.
Atrisinājums
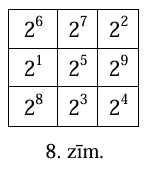
To var izdarīt, piemēram, tā, kā parādīts 8.zīm.
Izmantojot pakāpju īpašību \(a^{x+y}=a^{x} \cdot a^{y}\), atrisinājumu var iegūt, tabulā ierakstot pakāpes ar vienādām bāzēm tā, lai kāpinātāju summa katrā rindiņā un katrā kolonnā būtu viena un tā pati.
Atrisinājums
Sākam ar parastu maģisko kvadrātu, kur katrā rindiņā, kolonnā (un pat diagonālē - kaut arī tas nav prasīts) skaitļu summas ir vienādas:
| 8 | 1 | 6 |
|---|---|---|
| 3 | 5 | 7 |
| 4 | 9 | 2 |
#PropertiesOfExponents Ja jāpāriet no summām uz skaitļu reizinājumiem, var katru no skaitļiem \(a\) aizstāt, piemēram ar divnieka (vai cita konstanta skaitļa) pakāpi \(2^a\) un izmantot pakāpes īpašību, ka \(2^a \cdot 2^b = 2^{a+b}\).
Mūsu gadījumā \(8\) pārvēršas par \(2^8 = 256\), \(1\) pārvēršas par \(2^1 = 2\) utt. Iegūstam šādu kvadrātu:
| 256 | 2 | 64 |
|---|---|---|
| 8 | 32 | 128 |
| 16 | 512 | 4 |
Šajā kvadrātā katrā rindiņā, kolonnā (un arī abās diagonālēs) skaitļu reizinājumi ir \(2^15 = 32768\).