LV.AMO.2019.11.1
Atrisināt nevienādību
\[\frac{(x-20)^{19} \cdot(x+4)}{\left(\sqrt{x^{2}+4}\right)\left(9-x^{2}\right)} \geq 0\]
Atrisinājums
Ievērojam, ka reizinātājs \(\sqrt{x^{2}+4}\) ir pozitīvs visām reālām \(x\) vērtībām, tātad tas neietekmē kreisās puses izteiksmes zīmi. Izteiksmei \((x-20)^{19}\) ir tāda pati zīme kā izteiksmei \((x-20)\). Katru polinomu, kas ietilpst nevienādības kreisās puses izteiksmē, pielīdzinām \(0\) un atrisinām iegūtos vienādojumus:
- \((x-20)^{19}=0\) jeb \(x=20\)
- \(x+4=0\) jeb \(x=-4\)
- \(9-x^{2}=0\) jeb \(x= \pm 3\)
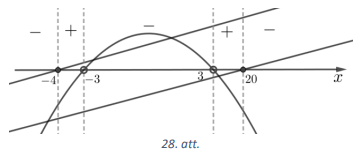
Iegūtās vērtības atliekam uz skaitļu ass, uzskicējam atbilstošo funkciju grafikus (skat. 28.att.) un nosakām dotās izteiksmes zīmi katrā intervālā. Tātad dotās nevienādības atrisinājums ir \(x \in[-4 ;-3) \cup(3 ; 20]\).