Atrisinājums

Turpinot virkni tālāk, iegūsim, ka tā ir (ar pelēkiem cipariem norādīts katra virknes locekļa nenulles ciparu reizinājums):

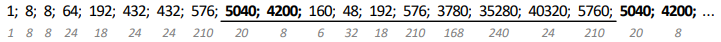
Tā kā katrs nākamais virknes loceklis ir atkarīgs no diviem iepriekšējiem virknes locekļiem, tad, līdzko parādās divi jau iepriekš bijuši skaitļi, izveidojas periods. Tā kā virknes devītais un desmitais loceklis ir \(5040\) un \(4200\), un \(19.\) un \(20.\) loceklis arī ir \(5040\) un \(4200\), tad virkne, sākot ar \(9.\) locekli, ir periodiska un perioda garums ir \(10\). Tāpēc pēdējais pilnais periods beidzas pie \(2018.\) virknes locekļa, jo \(2018=8+10 \cdot 201\), un \(2018.\) loceklis ir periodā pēdējais, tātad tas ir \(5760\).