LV.AMO.2018.7.3
Uz trijstūra \(ABC\) malas \(AB\) izvēlēts patvaļīgs iekšējs punkts \(D\). Pierādīt, ka \(CD>\frac{1}{2}(CA+CB-AB)\).
Atrisinājums
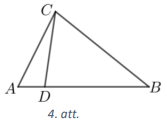
Izmantojot trijstūra nevienādību trijstūros \(ADC\) un \(BDC\) (skat. 4.att.), iegūstam
\[\begin{gathered} (CD+AD)+(CD+BD)>CA+CB \\ 2CD+AB>CA+CB \\ 2CD>CA+CB-AB \\ CD>\frac{1}{2}(CA+CB-AB) \end{gathered}\]