LV.AMO.2017.7.3
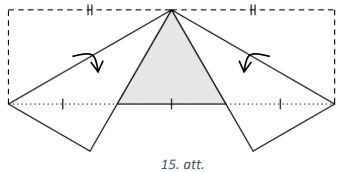
Divus taisnstūra lapas stūrus nolocīja tā, kā parādīts 15.att. Izrādījās, ka lapas apakšējā mala tika sadalīta trīs vienāda garuma nogriežņos un augšējā mala - divos vienāda garuma nogriežņos. Pierādīt, ka iekrāsotais trijstūris ir vienādmalu!
Atrisinājums
Tā kā trijstūris \(ABG\) sakrīt ar trijstūri \(AEG\), tad leņķis \(\sphericalangle BGA=\sphericalangle EGA\) (skat. 16.att.). Taisnstūra pretējās malas \(BC\) un \(AD\) ir paralēlas, tāpēc \(\sphericalangle BGA=\sphericalangle GAH\) kā iekšējie škērsleņķi pie paralēlām taisnēm. Līdz ar to \(\sphericalangle EGA=\sphericalangle GAH\) un trijstūris \(AHG\) ir vienādsānu un \(AH=GH\). Līdzīgi iegūstam, ka \(DI=IG\). Tā kā \(AH=HI=ID\), tad \(GH=HI=IG\) un trijstūris \(HGI\) ir vienādmalu.