Atrisinājums

Apzīmējam \(\sphericalangle ABC=\sphericalangle ACB=\alpha\) (skat. A8.att.).

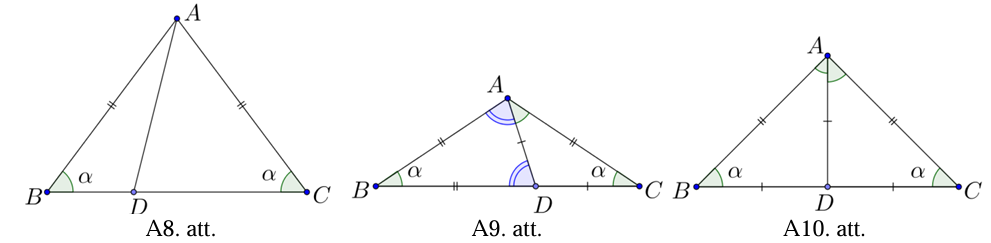
Apskatām vienādsānu trijstūri \(ABD\). Iespējami trīs gadījumi, kuras ir šī trijstūra vienādās malas.

1) Ja \(AB=AD\), tad punkts \(D\) nav \(BC\) iekšējs punkts. 2) Ja \(BD=AB\), apskatām vienādsānu trijstūri \(ACD\). Iespējami trīs gadījumi, kuras ir šī trijstūra vienādās malas.

2.1) Ja \(AD=AC\), tad punkts \(D\) nav \(BC\) iekšējs punkts.

2.2) Ja \(AC=CD\), tad \(AB+AC=BC\), kas ir pretrunā ar trijstūra nevienādību.

2.3) Ja \(AD=CD\) (skat. A9.att.), tad \(\sphericalangle ADC=180^{\circ}-2 \alpha\) un \(\sphericalangle BDA=\sphericalangle BAD=2\alpha\). Tad no \(\triangle BAD\) iekšējo leņķu summas izriet, ka \(\alpha+2 \alpha+2 \alpha=180^{\circ}\) jeb \(\alpha=36^{\circ}\). Līdz ar to trijstūra \(ABC\) leņķi ir \(\sphericalangle ABC=\sphericalangle ACB=36^{\circ}\) un \(\sphericalangle BAC=108^{\circ}\).

3) Ja \(AD=BD\), apskatām vienādsānu trijstūri \(ACD\). Iespējami trīs gadījumi, kuras ir šī trijstūra vienādās malas.

3.1) Ja \(AD=AC\), tad punkts \(D\) nav \(BC\) iekšējs punkts.

3.2) Ja \(AC=CD\), tad simetrijas dēļ šis gadījums ir analogs 2.3) gadījumam.

3.3) Ja \(AD=CD\), tad \(\sphericalangle ABD=\sphericalangle ACB=\sphericalangle CAD=\sphericalangle BAD=\alpha\) (skat. A10.att.). No \(\triangle ABC\) iekšējo leņķu summas izriet, ka \(4 \alpha=180^{\circ}\) jeb \(\alpha=45^{\circ}\). Līdz ar to trijstūra \(ABC\) leņķi ir \(\sphericalangle ABC=\sphericalangle ACB=45^{\circ}\) un \(\sphericalangle BAC=90^{\circ}\).