Atrisinājums

Ievērojam, ka trijstūra mediāna vienmēr atrodas trijstūra iekšpusē, bet augstums var atrasties arī ārpus trijstūra. Iespējami vairāki gadījumi, kā var būt novietots augstums \(BD\) un mediāna \(BE\) :

• Punkti \(D, A, E, C\) ir tieši šādā secībā (skat. A5.zīm.). No nogriežņu garuma īpašībām seko, ka \(EC=CD-ED=5-4=1 \mathrm{~cm}\). Tā kā \(BE\) ir mediāna, tad \(AC=2 \cdot EC=2 \cdot 1=2 \mathrm{~cm}\).

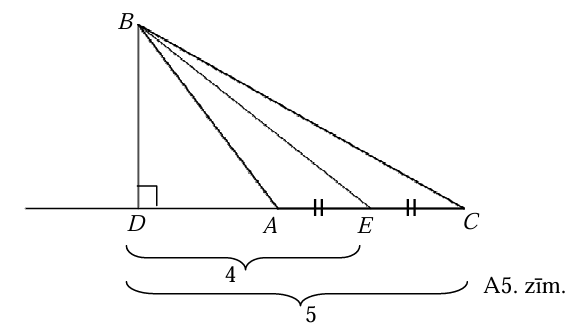
• Punktu secība \(A, D, E, C\) nav iespējama, jo tad \(EC=CD-DE=5-4=1\) \((cm)\) un \(AC=2 \mathrm{~cm}\). No otras puses \(AC=AD+DC=AD+5 > 5\). Iegūta pretruna.
• Punkti \(A, E, D, C\) ir tieši šādā secībā (skat. A6.zīm.). No nogriežņu garuma īpašībām seko, ka \(EC=ED+DC=5+4=9 \quad\) (cm). Tā kā \(BE\) ir mediāna, tad \(AC=2 \cdot EC=2 \cdot 9=18 \mathrm{~cm}\).

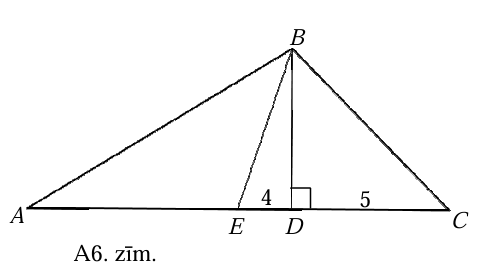
• Punktu secība \(A, E, C, D\) nav iespējama, jo tad \(ED=EC+CD=EC+5 > 4\).

Līdz ar to \(AC\) garums ir \(2~ \mathrm{cm}\) vai \(18~ \mathrm{cm}\).