LV.AMO.2010.7.2
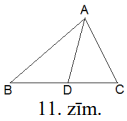
Caur trijstūra \(ABC\) virsotni \(A\) novilktā taisne \(t\) sadala trijstūri divos vienādos trijstūros.
Vai var gadīties, ka \(AB>AC\) ?
Atrisinājums
Taisne \(t\) krusto malu \(BC\) kādā iekšējā punktā \(D\) (ja tā nekrustotu pretējo malu, tad sākotnējais trijstūris netiktu sadalīts divos trijstūros). Pieņemsim, ka var gadīties, ka \(AB>AC\).
Tā kā trijstūri \(ABD\) un \(ADC\) ir vienādi, tad to attiecīgajām malām jābūt vienādām. Tā kā \(AB>AC\), tad jābūt \(AB=DC\) vai arī \(AB=AD\).
Ja \(AB=AD\), tad \(\triangle ABD\) ir vienādsānu, tātad arī tam vienādais
\(\triangle ACD\) arī ir vienādsānu trijstūris un \(AD=DC\) (nevar būt \(AD=AC\), jo
\(AD=AB>AC\)). Tātad \(AC=DB\). Iegūstam, ka \(BC=BD+DC=AC+AB\), kas ir pretrunā ar
trijstūra nevienādību \(BC
Ja \(AB=DC\), tad \(AC=BD\), vai arī \(AC=AD\), otrajā gadījumā \(\triangle ACD\) arī ir vienādsānu trijstūris, tātad jābūt \(AC=AD=BD\). Atkal iegūstam, ka \(BC=AC+AB\), kas ir pretrunā ar trijstūra nevienādību.
Esam apskatījuši visas iespējas, tātad nevar gadīties, ka \(AB>AC\).