LV.AMO.2009.7.4
Trijstūris \(ABC\) ir šaurleņķu. Trijstūri \(AMB\) un \(BNC\) abi ir vienādmalu un atrodas ārpus \(\triangle ABC\). Pierādīt, ka \(AN=CM\).
Atrisinājums
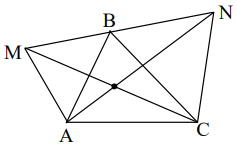
Tā kā \(AB=MB\), \(BN=BC\) un \(\sphericalangle ABN= \sphericalangle ABC +60^{\circ}=\sphericalangle MBC < 150^{\circ}\), tad \(\triangle ABN=\triangle MBC\ (m \ell m)\). Tāpēc \(AN=MC\).